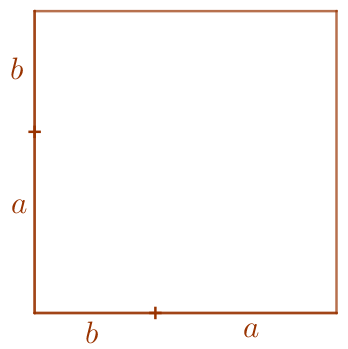
La moyenne géométrique de deux nombres positifs est inférieure ou égale à leur moyenne arithmétique.
 |
 |
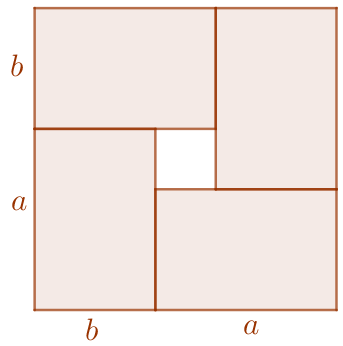 |
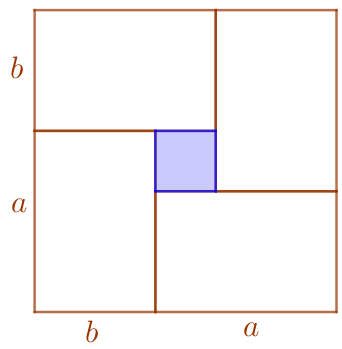
L’aire du grand carré est supérieure à celle du petit carré bleu : ![]()
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)

La moyenne géométrique de deux nombres positifs est inférieure ou égale à leur moyenne arithmétique.
 |
 |
 |
L’aire du grand carré est supérieure à celle du petit carré bleu : ![]()