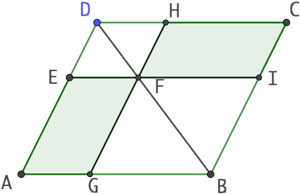
La diagonale d’un parallélogramme et deux droites parallèles à deux cotés du parallélogrammes et sécantes ensemble avec la diagonale, construisent deux parallélogramme de même aire. Dans la figure ci-contre les parallélogrammes FEAG et FICH ont la même aire.
Explications :
La diagonale (DB) coupe ABCD en deux triangles ABD et DBC de même aire : 
. (1)
La diagonale (DF) coupe DEFH en deux triangles DEF et DFH de même aire : 
.
La diagonale (FB) coupe FGBI en deux triangle FGB et FBI de même aire : 
.
L’égalité (1) devient : 
.
En simplifiant il reste : 
.
Remarque : Il s’agit de la proposition I.43 des Éléments d’Euclide.
