On va découper en deux parties le segment [AB]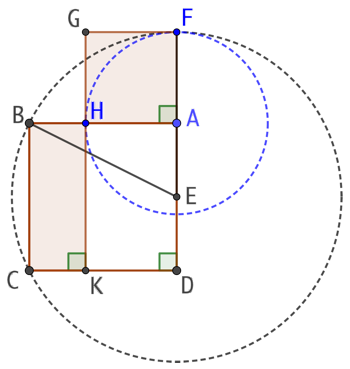
de manière à construire un rectangle et un carré de même aire.
Construction :
- On construit le carré ABCD.
- On place le point E milieu de [AD].
- On trace le cercle de centre E et de rayon EB.
- Ce cercle coupe la droite (DA) au point F.
- On trace le cercle de centre A et de rayon AF.
- Ce cercle coupe la droite (AB) au point H.
- Le carré AFGH et le rectangle BCKH ont la même aire.
Explications :
Prenons AB comme unité de mesure. 
.
En considérant le triangle ABE rectangle en A, on obtient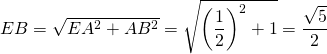 
.
.
L’aire du carré AFGH est :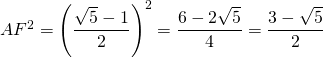 
.
L’aire du rectangle BCKH est 
puisque 
.
.
Donc les deux aires sont identiques.
Remarque : Il s’agit de la proposition II.11 des Éléments d’Euclide.
