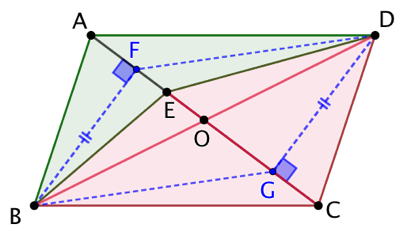
Soit ABCD un parallélogramme. Où placer le point E à l’intérieur de ABCD pour que BCE, ECD et ABED aient la même aire ?
Explications :
On oublie le quadrilatère ABED. On va chercher le lieu des points E tels que les les triangles BCE et CDE aient la même aire.
Soient F et G les pieds respectifs des hauteurs issues de B et D des triangles BCE et CDE. Les droites (FB) et (GD) sont parallèles car perpendiculaires toutes les deux avec (EC). Par ailleurs FB = GD puisque BCE et CDE ont la même aire. Par conséquent BGDF est un parallélogramme.
Donc les diagonales de BGDF, (BD) et (FG) se coupent en leur milieu O. Or, ABCD est aussi un parallélogramme. Donc ses diagonales (BD) et (AC) se coupent en leur milieu O. O appartient donc à (FG), c’est à dire à (EC). Par conséquent les droites (AC) et (EC) ont deux points en commun : O et C; elles sont donc égales, ce qui permet d’affirmer que E appartient à la diagonale (AC).
Réintroduisons ABED dans la démonstration. (AC) coupe ABCD en deux triangles de même aire et les triangles BCE et ECD ont la même aire. Par conséquent les triangles ABE et AED ont la même aire. On recherche donc un point E tel que l’aire de BCE soit le double de celle de ABE. Comme ces deux triangles ont la même hauteur, il suffit que 
.
Autre article : Dans le cas particulier où ABCD est un carré.
