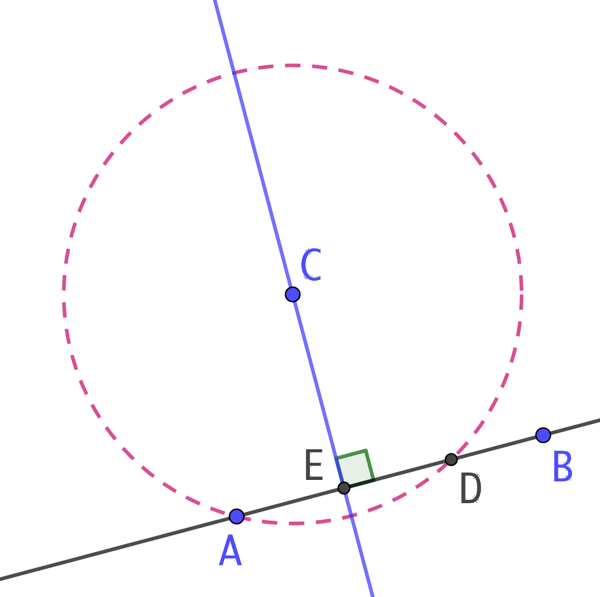
Soit la droite (AB) et un point C n’appartenant pas à cette droite. La droite perpendiculaire à (AB) passant par C se construit ainsi :
- On trace un cercle de centre C en choisissant le rayon de telle manière que le cercle coupe (AB) en deux points distincts. On peut par exemple choisir un cercle passant par A.
- Ce cercle coupe également (AB) au point D.
- ll suffit alors de tracer la médiatrice de [AD]. Ce sera la perpendiculaire à (AB) passant par C, à savoir la droite (CE).
Explications :
Les points A et D appartiennent au cercle de centre C, donc les distances CA et CD sont égales. Par conséquent C appartient à la médiatrice de [AD]. Or la médiatrice de [AB] est une droite perpendiculaire à ce segment. Comme elle passe par C, c’est bien la droite que nous recherchons.
Remarque : Il s’agit de la proposition I.12 des Éléments d’Euclide.
Remarque : La construction proposée dans cet article est plus rapide : Perpendiculaire d’une droite passant par un point (version 3)
