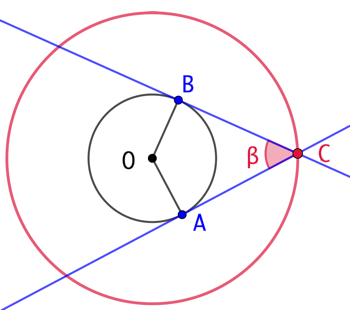
Soient un cercle de centre O et une mesure d’angle 
fixée. Soit C un point extérieur au cercle tel que les deux tangentes au cercle passant par C fassent entre elles un angle de mesure . Le lieu géométrique des points ayant la même propriété que C est un cercle de centre O.
Explications :
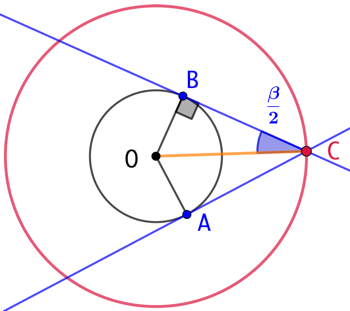
Par construction, le point O est équidistant des droites (CB) et (CA), donc la droite (CO) est la bissectrice de l’angle 
. Par conséquent 
.
Puisque est une mesure d’angle constante, 
est constant. Or 
Donc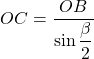 
.
Comme OB est un rayon du cercle de centre O, sa valeur est constante. On en conclut que la valeur de la distance OC est constante, donc que C décrit un cercle de centre O.
