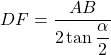Soient deux segments [AB] et [BC], ainsi que deux mesures d’angle 
et 
. On veut placer un point H tel que depuis ce point, [AB] et [BC] soient respectivement vus sous des angles de mesure et .
 |
 |
 |
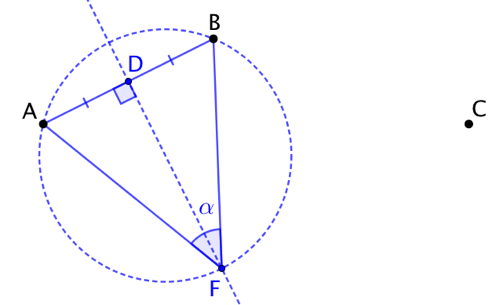
| On construit les deux arcs de cercle depuis lesquels [AB] et [BC] soient vus sous des angles de mesure et .
Pour [AB], on commence par positionner le point F de la médiatrice duquel [AB] est vu avec un angle de mesure Puis on trace l’arc de cercle AFB. |
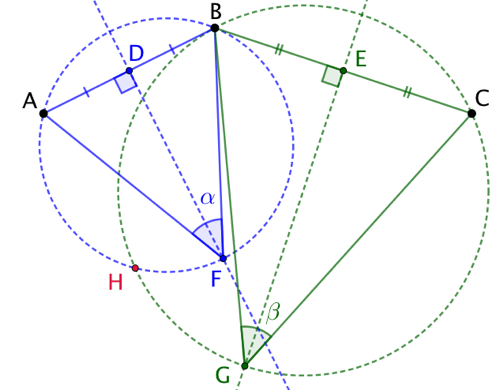
On fait de même pour tracer l’arc de cercle BGC. On démontre que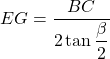 
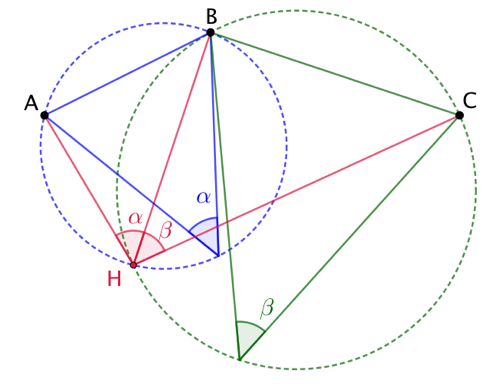
L’intersection des deux arcs de cercles est le point recherché H. |
|
