Forme bilinéaire symétrique définie positive
![]() une application de
une application de ![]() dans
dans ![]() est une FBDP si et seulement si :
est une FBDP si et seulement si :
- bilinéaire : linéaire par rapport à chaque variable :
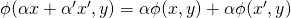
- symétrique :
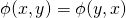
- définie :
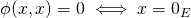
- positive :
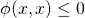
Un espace vectoriel ![]() muni d’un produit scalaire est un espace préhilbertien réel. Si
muni d’un produit scalaire est un espace préhilbertien réel. Si ![]() de dimension finie, c’est un espace euclidien.
de dimension finie, c’est un espace euclidien.
Dans la suite on se situera dans un espace préhilbertien réel.
Norme euclidienne
Application de ![]() dans
dans ![]() , qui à
, qui à ![]() associe
associe ![]()
Égalité du parallélogramme : ![]()
Inégalité de Cauchy-Schwarz (Égalité si les vecteurs sont colinéaires) : ![]()
Inégalité triangulaire : ![]()
Orthogonalité
Théorème de Pythagore : ![]()
Parties orthogonales : ![]()
L’orthogonal de ![]() :
: ![]()
![]() est un SEV de
est un SEV de ![]()
![]()
Si ![]() alors
alors ![]()
![]()
![]() est une famille orthogonale si et seulement si
est une famille orthogonale si et seulement si ![]()
Toute famille orthogonale composée de vecteurs tous non nuls est libre.
Une famille orthonormale est une famille orthogonale dont les tous les éléments ont une norme unitaire.