I – Grandeurs proportionnelles

Définition

Deux grandeurs sont proportionnelles lorsque les valeurs de l’une s’obtiennent en multipliant (ou en divisant) par un même nombre non nul les valeurs de l’autre.

Exemple :

Dans l’aviation, on mesure l’altitude en « pied » et non en mètre. Un pied correspond à 0,3048 mètre. Pour convertir en mètres une longueur exprimée en pieds, on la multiplie par 0,3048. Dire qu’un avion vole à 10 000 pieds est équivalent à dire qu’il vole à 3 048 m car $10\:000 \times 0,3\:048 = 3\:048$ .

Les deux grandeurs, exprimées en pied et en mètre, sont donc proportionnelles. Le nombre 0,3 048 est appelé coefficient de proportionnalité.

ATTENTION : Deux grandeurs ne sont pas toujours proportionnelles. En voici quelques-unes qui ne le sont pas :

La taille d’une personne et son âge ;
l’aire d’un carré et la longueur de son côté.

II – Calculs dans une situation de proportionnalité

Pour illustrer une situation de proportionnalité, on utilise souvent un tableau appelé tableau de proportionnalité. Dans un tel tableau, on obtient les nombres de la seconde ligne en multipliant ceux de la première ligne par le coefficient de proportionnalité.

Exemple : Comment complèter le tableau de proportionnalité suivant ?

Si on ne nous donne pas le coefficient de proportionnalité, il faut commencer par le calculer.

D’après le tableau de proportionnalité, on sait que 8 kg de pommes coûtent 7,68 €. On cherche le coefficient de proportionnalité, c’est-à-dire le nombre manquant dans la multiplication : $8 \times \cdots = 7,68$ . Ce nombre est égal à $7,68 \div 8 = 0,96$ . Cela signifie qu’un kilogramme de pommes coûte 0,96 €. Donc

deux kilogrammes coûtent 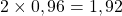$2 \times 0,96 = 1,92 €$ et
24 kilogrammes coûtent $24 \times 0,96 = 23,04 €$ .

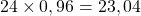On peut partiellement compléter le tableau de proportionnalité :

Pour remplir les deux cases de la première ligne, on peut remarquer qu’on peut acheter un kilogramme de pommes avec 0,96 €. Donc combien de kilogrammes peut-on acheter avec 9,60 € ? Il suffit de faire la division $9,6 \div 0,96 = 10$ . On peut donc acheter 10 kilogrammes de pommes avec 9,60 €.

De la même façon : Combien de kilogrammes peut-on acheter avec 15,36 € . On fait la division : $15,36 \div 0,96 = 16$ . On peut donc acheter 16 kilogrammes de pommes avec 15,36 €.

Le tableau de proportionnalité complet est :

Remarque : Dans un le tableau de proportionnalité, on obtient les nombres de la première ligne en divisant ceux de la seconde ligne par le coefficient de proportionnalité.

III – Reconnaître une situation de proportionnalité

Question : Comment être certain que le tableau que l’on vous propose est un tableau de proportionnalité, qui décrit une situation de proportionnalité ?

Réponse : il faut prendre chaque nombre de la seconde ligne et le diviser par le nombre qui lui correspond dans la première ligne. Si tous les calculs donnent le même résultat, on est certain qu’il s’agit d’un tableau de proportionnalité.

Exemples :