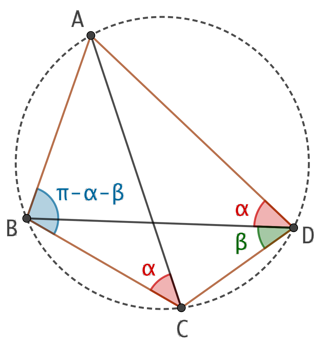
Quadrilatère inscriptible ou cyclique

Un quadrilatère inscriptible ou cyclique est un quadrilatère dont les quatre sommets sont cocycliques.

Deux propriétés :

ABCD est inscriptible si et seulement si $\widehat{ADB}=\widehat{ACB}.$
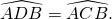
ABCD est inscriptible si et seulement si les angles opposées sont supplémentaires, c’est à dire $\widehat{ADC}+\widehat{CBA}=\pi$

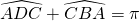
Les explications : voir les articles sur les angles inscrits et sur les points cocycliques.

Remarque : Il s’agit des propositions III.21 et III.22 des Éléments d’Euclide.