Étant données deux droites d1 et d2 sécantes et un point E n’appartenant à aucune d’entre elles, construire un segment [AB] tel que A et B soient respectivement situés sur d1 et d2, et E milieu de [AB].
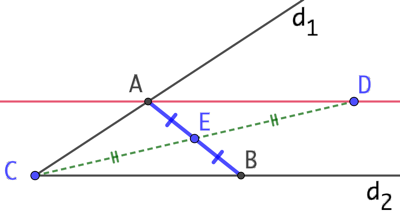
Première construction :
- Soit C le point d’intersection de d1 et d2. On construit D symétrique de C par rapport à E.
- On trace la droite parallèle à d2 passant par D. Elle coupe d1 en A.
- On construit B le symétrique de A par rapport à E. B appartient à d2.
Explications :
Par construction, les diagonales du quadrilatère ACBD se coupent en leur milieu E, donc ACBD est un parallélogramme. Alors les droites (AD) et (CB) sont parallèles. Or (AD) est par construction parallèle à d2 et C appartient à d2, donc B appartient aussi à d2.
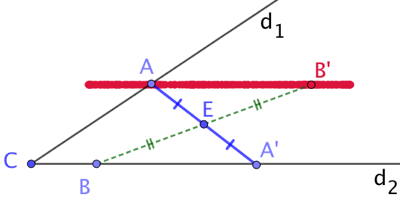Deuxième construction :
- On abandonne provisoirement la condition “A appartient à d1“. On place un point B quelconque sur d2.
- Soit B’ le symétrique de B par rapport à E.
- Quand B parcourt la droite d2, B’ décrit la droite symétrique de d2 par rapport à E. (on a activé le mode “trace” de Geogebra pour obtenir la droite rouge).
- Cette droite rencontre la droite d1 au point A. On construit le point A’ symétrique de A par rapport à E. Ce point A’ est le point B recherché.
Explications :
L’image d’une droite par rapport à un point est une droite parallèle, donc d2 et (AB’) sont parallèles. Si A’ est l’image de A par cette même symétrie de centre A, alors nécessairement A’ est sur la droite d2 et E est le milieu de [AA’].
Remarque : On aurait obtenu le même résultat en abandonnant provisoirement la condition “B appartient à d2” et en faisant parcourir un point A sur d1.
