Somme de carrés dans un rectangle

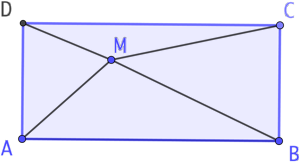
Étant donnés un rectangle ABCD et un point quelconque M situé dans le rectangle, on démontre l’égalité suivante :

MA² + MC² = MB² + MD²

Explications :

On complète la figure en plaçant les points E, F, G et H, projections orthogonales respectives de M sur [AB], [BC], [CD] et [DA]. On utilise le théorème de Pythagore :

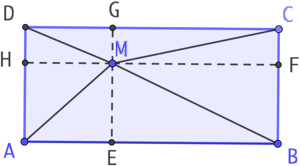
• MA² = MH² + HA² = MH² + FB²
• MB² = MF² + FB²
• MC² = MF² + FC² = MF² + HD²
• MD² = MH² + HD²
• MA² + MC² = MH² + FB² + MF² + HD²
• MB² + MD² = MF² + FB² + MH² + HD²

Donc MA² + MC² = MB² + MD²

Remarque : Cette égalité reste vraie si M se situe en dehors du rectangle. On le démontre encore avec Pythagore.