La rigueur mathématique imposerait de raisonner avec des mesures algébriques. Par commodité, on se limite ici à des angles ![]() et
et ![]() positifs et inférieurs à 90°.
positifs et inférieurs à 90°.
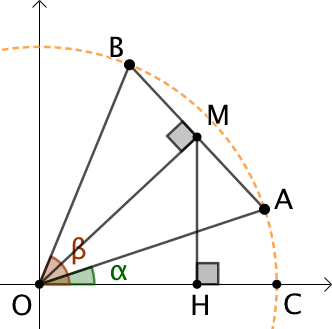 Dans le cercle unitaire, soient les angles
Dans le cercle unitaire, soient les angles ![]() et
et ![]() de mesures respectives
de mesures respectives ![]() et
et ![]() . Alors les coordonnées respectives de A et de B sont
. Alors les coordonnées respectives de A et de B sont ![]() et
et ![]()
Soit M le milieu du segment [AB]. Alors les coordonnées de M sont ![]() .
.
Le triangle OAB est isocèle puisque ![]() Donc la droite (OM) est à la fois une bissectrice et une médiatrice issue de O. L’angle
Donc la droite (OM) est à la fois une bissectrice et une médiatrice issue de O. L’angle ![]() mesure
mesure ![]() . Par conséquent :
. Par conséquent : ![]()
Soit H le projeté orthogonal de M sur l’axe des abscisses.![]() .
. ![]() mesure
mesure ![]() . Par conséquent la mesure de
. Par conséquent la mesure de ![]() est
est ![]()
Alors ![]() .
.
Par ailleurs ![]() .
.
OH et HM sont les coordonnées du point M, exprimées précédemment. Cela donne donc :
Voir : Sinus et cosinus de sommes
