Soit ![]() une suite algébrique de premier terme
une suite algébrique de premier terme ![]() et de raison
et de raison ![]() . Montrer que la suite
. Montrer que la suite ![]() définie pour tout entier naturel
définie pour tout entier naturel ![]() par
par ![]() est géométrique.
est géométrique.
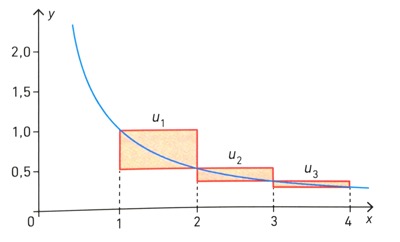
On considère la fonction ![]() définie sur
définie sur ![]() par
par ![]() , dont la courbe représentative est donnée ci-dessous. À partir de la fonction
, dont la courbe représentative est donnée ci-dessous. À partir de la fonction ![]() , on définit, pour tout entier
, on définit, pour tout entier ![]() , la suite
, la suite ![]() comme indiqué ci-dessous.
comme indiqué ci-dessous.
![]() est l’aire du premier rectangle rouge ;
est l’aire du premier rectangle rouge ;
![]() est l’aire du deuxième rectangle rouge ;
est l’aire du deuxième rectangle rouge ;
![]() est l’aire du troisième rectangle rouge ;
est l’aire du troisième rectangle rouge ;
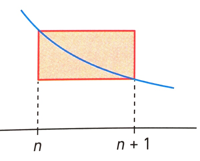
![]() est l’aire du n-ième rectangle rouge.
est l’aire du n-ième rectangle rouge.
- Donner une définition explicite pour
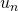 .
. - Calculer
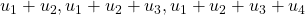 .
. - Calculer
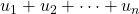 .
.
On considère la suite ![]() définie par
définie par ![]() et
et ![]() .
.
- Calculer
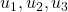
- La suite
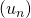 est-elle arithmétique, géométrique ?
est-elle arithmétique, géométrique ? - On pose
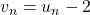 . Démontrer que la suite
. Démontrer que la suite 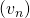 est géométrique de raison
est géométrique de raison 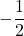 .
. - Déduire de la question précédente l’expression de
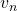 en fonction de
en fonction de 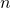 .
. - Déterminer
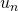 en fonction de
en fonction de 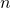 .
.
Indiquer si chaque suite donnée ci-dessous, est géométrique ou non. Justifier votre réponse.
Une suite arithmétique est telle que ![]() et
et ![]() .
.
- déterminer sa raison et son premier terme.
- Calculer
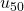 .
.
Calculer ![]() .
.
On considère la suite ![]() définie par
définie par ![]() et
et ![]() .
.
- Calculer
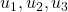
- On définit la suite
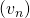 par
par 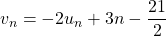 . Démontrer que la suite
. Démontrer que la suite 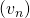 est une suite géométrique dont donnera la raison et le premier terme.
est une suite géométrique dont donnera la raison et le premier terme. - En déduire que, pour tout entier naturel
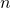 ,
, 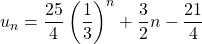 .
. - Soit
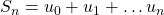 . Déterminer l’expression de
. Déterminer l’expression de 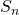 en fonction de
en fonction de 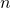 .
.
