 |
 |
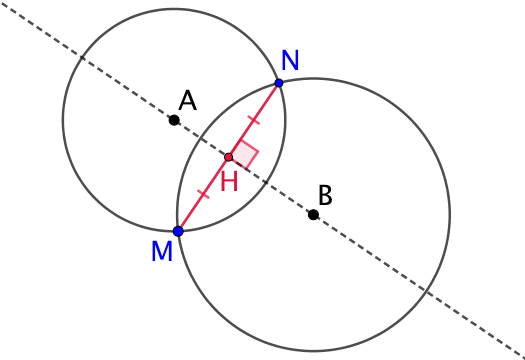 |
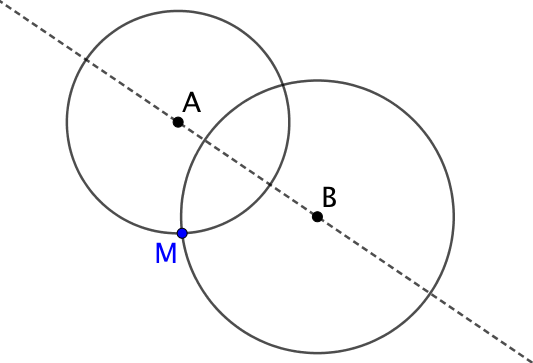
| On cherche le symétrique de M par rapport à (AB). | On trace les cercles de centres respectifs A et B passant par M. | La seconde intersection de ces deux cercles est le point N, symétrique de M par rapport (AB). |
Explications : Par construction AN = AM et BN = BM. Donc (AB) est la médiatrice de [MN]. Par conséquent (MN) et (AB) sont perpendiculaires. La médiatrice (AB) coupe le segment [MN] en son milieu H. MH = NH. Donc M et N sont symétriques par rapport à (AB).
