 |
 |
 |
| On veut construire le symétrique de M par rapport à A. |
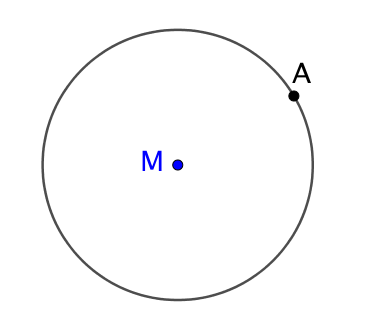
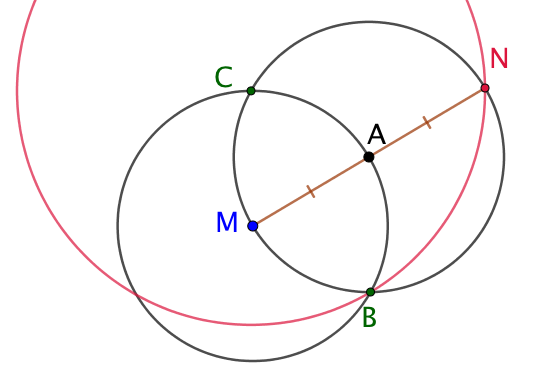
On trace le cercle de centre M passant par A. |
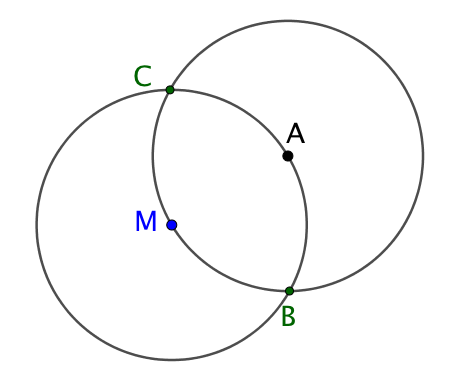
On trace le cercle de centre A passant par M. Les deux cercles se coupent en B et C. |
 |
 |
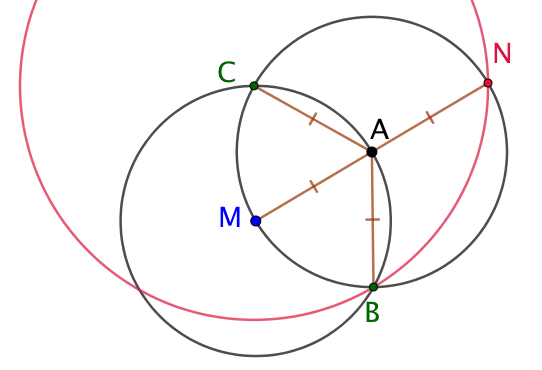 |
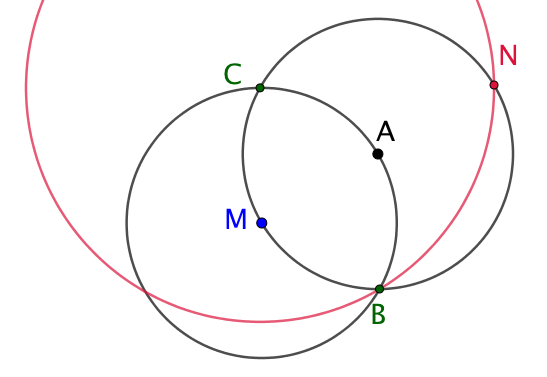
| On trace le cercle de centre C passant par B. Il coupe le cercle de centre A en N. N est le symétrique de M par rapport A. |
Les points M et N sont sur le cercle de centre A donc AM = AN. |
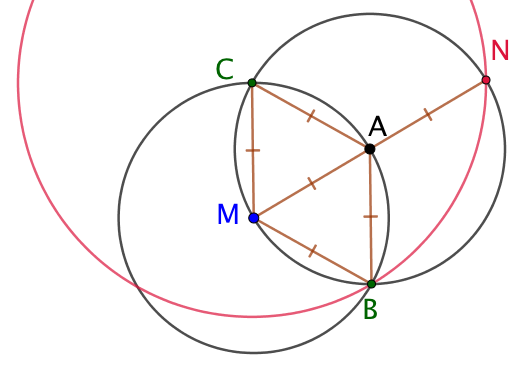
Les points B et C sont sur le cercle de centre A. Donc AC = AB. Par conséquent A est sur la médiatrice de [BC]. |
 |
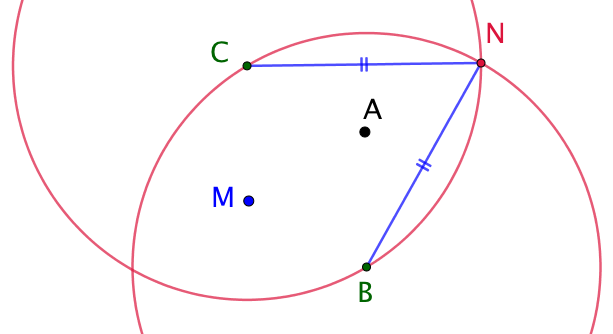 |
Conclusion : les points M, A et N sont alignés. On a vu que AM = AN. On a ainsi démontré que M et N sont symétriques par rapport à A. |
| Les points B et C sont sur le cercle de centre M. Donc MC = MB. Par conséquent M est sur la médiatrice de [BC]. |
On trace le cercle de centre B passant par C. Donc NB = NC. Par conséquent N est sur la médiatrice de [BC]. |









