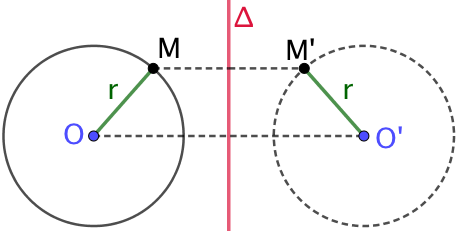
Le symétrique axiale d’un cercle est un cercle de même rayon et dont le centre est le symétrique axial du centre du cercle d’origine.
Explications :
Soient un axe 
et un cercle de centre O et de rayon r. Soit O’ le symétrique axial de O par rapport à .
Soit M un point de ce cercle et M’ son symétrique axial par rapport à . On sait alors que le symétrique axial du segment [OM] et le segment [O’M’] et que OM’ = OM = r.
Donc le symétrique axial de M est un point du cercle de centre O’ et de rayon r. On en conclut que l’image du cercle de centre O et de rayon r est inclus dans le cercle de centre O’ et de rayon r’. On démontre très facilement que l’image du cercle de centre O’ et de rayon r est inclus dans le cercle de centre O et de rayon r’.
