Le symétrique axial d’un segment est un segment de même longueur dont les extrémités sont les images axiales des extrémités du segment d’origine.
Explications :
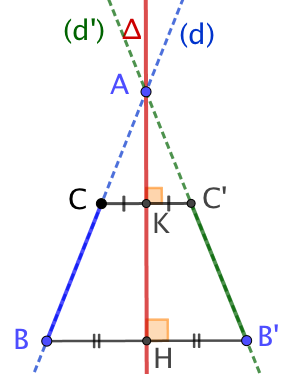
On considère un axe 
. Soit le segment [CD] porté par la droite (d). On sait que l’image de [CD] est porté par la droite (d’) image de (d) par rapport à . On démontre sans peine avec le théorème de Thalès que l’image de tout point de [BC] est situé dans [B’C’]. Reste à démontrer que BC = B’C’.
Soit A le point d’intersection de (d) et (d’), et évidemment de .
est la médiatrice de [BB’] et de [CC’]. Donc AB = AB’ et AC = AC’. Comme AB = AC + CB et AB’ = AC’ + C’B’, il vient que CB = C’B’.
