Tangente au cercle à partir d’un point extérieur au cercle

Etant donnés un cercle de centre O et un point A n’appartenant pas à ce cercle, on construit la tangente passant par A ainsi :

1. On place le point C milieu du segment [OA].
2. On trace le cercle de centre C passant par A et donc aussi par O.
3. Ce cercle coupe le cercle de centre O aux points D et E.
4. Les droites (AD) et (AE) sont les deux tangentes recherchées.

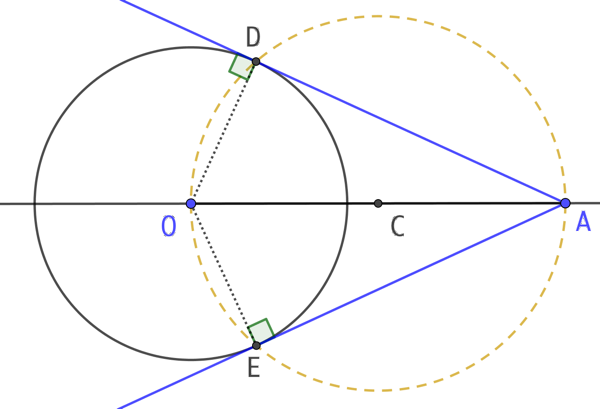
Explications :

Le cercle de centre C milieu de [OA] coupe le cercle de centre O en D et en E. D appartient au cercle de diamètre [OA] donc ODA est un triangle rectangle en D. Ainsi (OD) et (DA) sont perpendiculaires, ce qui permet de conclure que (DA) est l’une des deux tangentes recherchées.

Même raisonnement pour E.