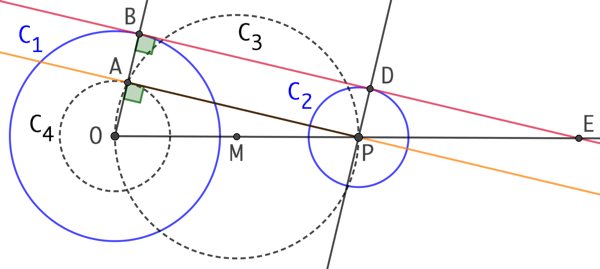
Étant donnés deux cercles C1 et C2, de centre respectif O et P, tel que le rayon de C1 soit supérieur à celui de C2; on construit ainsi les deux tangentes extérieures à ces deux cercles :
- On place le point M milieu du segment [OP] et on trace le cercle C3 de centre M passant par O.
- On trace le cercle C4 de centre O et de rayon égal à la différence des rayons des deux cercles donnés.
- Soit A le point d’intersection de C3 et de C4. On trace la droite (OA). Elle coupe C1 au point B.
- La tangente à C1 en B est la tangente à C2 en D.
- Le procédé de construction de la seconde tangente, située en dessous des cercles est identique.
Explications :
A est sur le cercle C3 de diamètre OP donc le triangle AOP est rectangle en A. Autrement dit les droites (OA) et (AP) sont perpendiculaires.
La droite (BE) tangente au cercle C1 est perpendiculaire à (OB), c’est-à-dire (OA). Par conséquent les droites (AP) et (BE) sont parallèles.
Soit D le point d’intersection de la droite (BE) et du cercle C2. Par hypothèse 
donc 
. Donc PD est égale à la distance entre les droites (AP) et (BE). Alors les droites (PD) et (BE) sont perpendiculaires, donc la droite (BE) est la tangente de C2 en D.
Remarque : en considérant le triangle OBE et en utilisant le théorème de Thales, on démontre que 
.
Remarque : il existe également deux tangentes communes qui passent entre ces deux cercles.
