Tangente et égalité d’angle

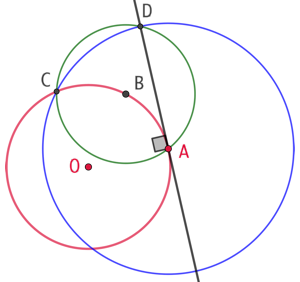
Autre scénario de construction de la tangente à un cercle en un point donné.

Construction : Soit un cercle de centre O et un point A de ce cercle.

• On choisit arbitrairement un autre point B du cercle et on trace le cercle de centre B passant par A.
• Les deux cercles se coupent au point C. On trace le cercle de centre A passant par C.
• Les cercles de centre A et B se coupent en un point D. La droite (AD) est la tangente au cercle en A.

Explications :

On va démontrer que les droites (OA) et (AD) sont perpendiculaires.

.

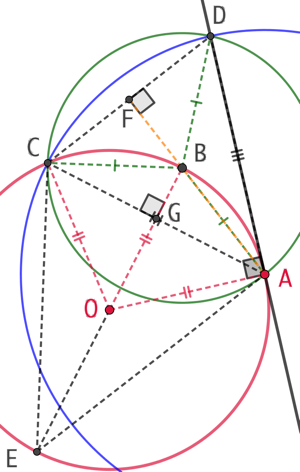Dans le triangle GOA : .

Donc .

Voir les articles :

• Angle inscrit et angle corde-tangente
• Hauteur d’un triangle rectangle

Autre résultat : La droite (AB) est la bissectrice de l’angle .

La droite (AG) est la hauteur issue de A du triangle rectangle ABE. Par conséquent les triangles GAB et ABE sont semblables. Donc .

Or et .

Par conséquent , ce qui démontre que (AB) est la bissectrice de .