Thales et moyenne géométrique

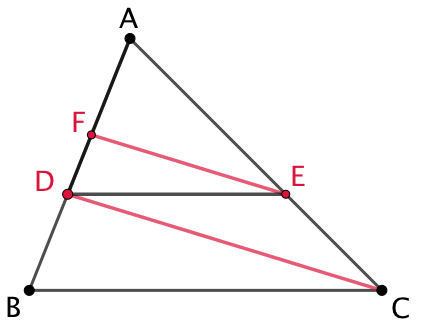
Soit un triangle ABC et un point D de l’intervalle [AB].  La droite parallèle à (BC) passant par D coupe (AC) en E. La droite parallèle à (CD) passant par E coupe (AB) en F. Alors AD est la moyenne géométrique de AF et de AB.

Explications : on utilise deux fois le théorème de Thalès

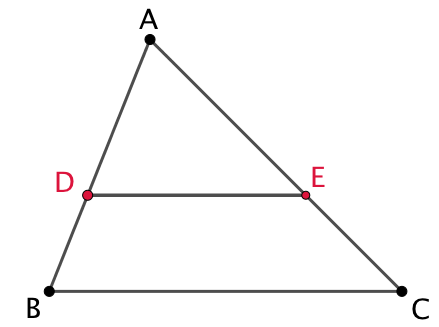
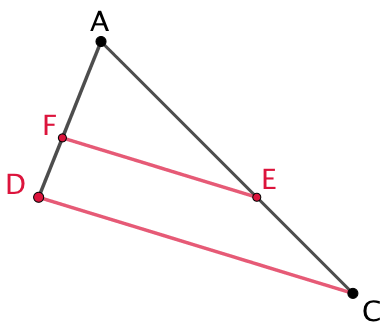
Par construction les droites (DE) et (BC) sont parallèles donc \dfrac{AD}{AB} = \dfrac{AE}{AC} Par construction les droites (CD) et (EF) sont parallèles donc \dfrac{AF}{AD} = \dfrac{AE}{AC}

Par conséquent : \dfrac{AD}{AB} = \dfrac{AF}{AD}. Ce qui permet de conclure que AD^2 = AB \times AF, doit AD = \sqrt{AB \times AF}.

Print Friendly, PDF & Email