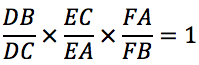Théorème de Ceva

Le théorème de Ceva donne une condition nécessaire et suffisante pour que trois droites passant par les trois sommets d’un triangle soient concourantes :

1ère partie : Supposons que les droites (AD), (BE) et (CF) soient concourantes en un point M.

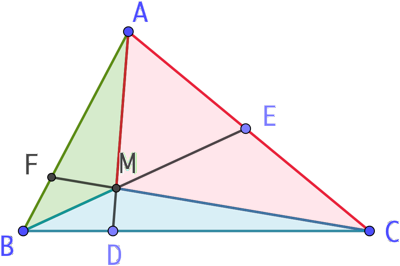Le lemme du chevron appliqué trois fois au triangle ABC donne :

\dfrac{Aire_{ABM}}{Aire_{AMC}} = \dfrac{DB}{DC}

\dfrac{Aire_{BCM}}{Aire_{BMA}} = \dfrac{EC}{EA}

\dfrac{Aire_{CBM}}{Aire_{CAM}} = \dfrac{FB}{FA}

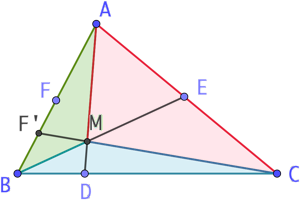Le produit des trois rapports des aires donne 1 donc \dfrac{DB}{DC} \times \dfrac{EC}{EA} \times \dfrac{FB}{FA} = 1.

2ème partie : supposons que \dfrac{DB}{DC} \times \dfrac{EC}{EA} \times \dfrac{FB}{FA} = 1

Supposons par ailleurs que (AD) et (BE) se coupent en un point M et que la droite (CF’) passe aussi par M. Montrons alors que F = F’.

Puisque les droites (AD), (BE) et (CF’) sont concourantes en M, nous avons le rapport : \dfrac{DB}{DC} \times \dfrac{EC}{EA} \times \dfrac{F'B}{F'A} = 1 = \dfrac{DB}{DC} \times \dfrac{EC}{EA} \times \dfrac{FB}{FA}

. En simplifiant il obtient l’égalité : \dfrac{F'B}{F'A} = \dfrac{FB}{FA}. Ce qui permet de conclure que F = F’.

Vérifions cela : \dfrac{F'B}{F'A} = \dfrac{FB}{FA} alors F'A \times FB = FA \times F'B Soit F'A \times (AB - AF) = FA \times (AB - AF'). Après développement et simplification par F'A \times AF, puis par AB. Il reste AF = AF' donc F=F'.

Print Friendly, PDF & Email