Soit un triangle ABC rectangle en B tel que AB = a, BC = b et CA = c. Pour démontrer 
, on utilise la construction suivante :
- On trace un cercle de centre C et de rayon c ;
- Soit D le second point d’intersection de (BA) et du cercle ;
- Soient E et F les points d’intersection de (BC) et du cercle ;
- Les triangles BFA et BED sont semblables ;
- On démontre l’égalité recherchée grâce à la proportionnalité entre les longueurs des côtés de ces deux triangles.
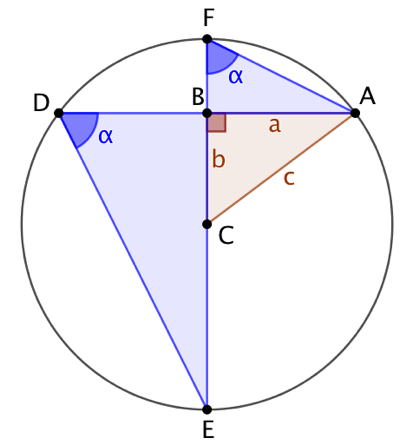Explications :
On remarque que les angles 
et 
interceptent le même arc de cercle AE. Ils ont donc la même mesure.
Comme BFA et BED sont rectangles en B et que 
, on en conclut qu’ils sont semblables et que les longueurs de leurs côtés sont proportionnels. Ce qui permet d’écrire :
ce qui donne 
soit 
c’est à dire : .
