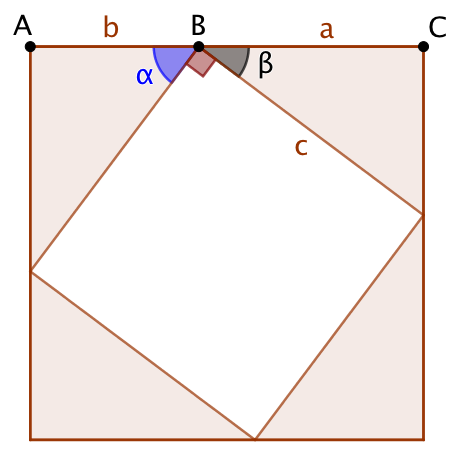
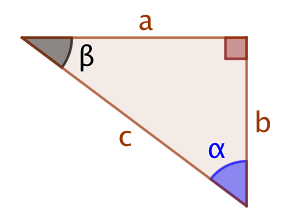
Soit un triangle rectangle dont les côtés mesurent 
, 
, et 
, c étant la longueur de l’hypoténuse. Pour démontrer que 
, on utilise la construction suivante :
- On trace un carré de côté ;
- On entoure ce carré par 4 triangles isométriques au triangle de départ ;
- On obtient un carré de côté
.
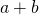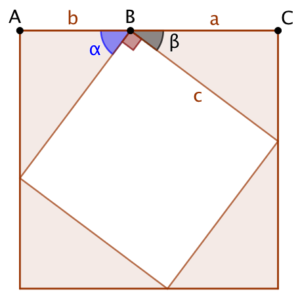Il faut d’abord prouver qu’on obtient bien quadrilatère. Pour cela on montre que les points A, B et C sont alignés : 
. Or dans le triangle rectangle de départ : 
. Par conséquent 
.
On calcule l’aire du grand carré de deux façons :
Calcul direct : 
Calcul par ajout d’aire : l’aire du grand carré est la somme de l’aire du petit carré et de celle de 4 triangles isométriques. Ce qui donne : 
.
On obtient alors l’égalité : 
, soit .
