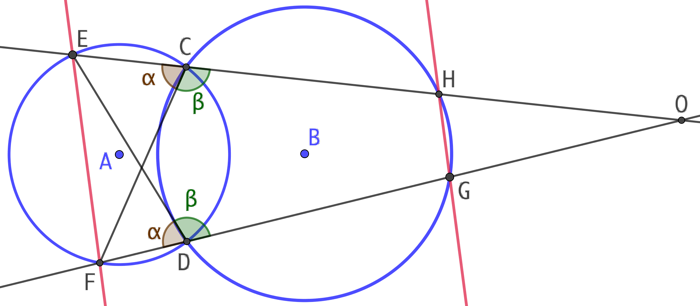
Étant donnés deux cercles de centre A et B se coupant aux points C et D, et E et F deux points quelconques choisis sur l’un des cercles, les droites (EC) et (FD) coupent le second cercle aux points G et H. On démontre que les droites (EF) et (HG) sont parallèles.
Explications :
car ces angles interceptent le même arc de cercle EF.
Donc 
.
On peut alors affirmer que : O étant le point d’intersections des droites (EC) et (FD), les triangles EDO et CFO sont semblables.
Ce qui permet d’écrire les égalités de rapports : 
, c’est-à-dire 
.
D’après la réciproque du théorème de Thales, cette dernière égalité valide que les droites (EF) et (HG) sont parallèles.
A. Reim (1832-1922) : géomètre sudète
