Dans un triangle rectangle, la hauteur issue de l’angle droit est la moyenne géométrique entre les projections des petits côtés sur l’hypoténuse.
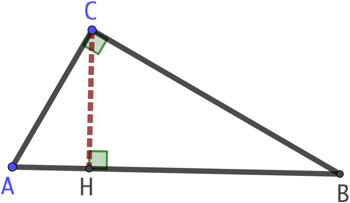
Soit un triangle ABC rectangle en C. (CH) est la hauteur issue de C. Elle coupe (AB) en H. H est de fait le projeté orthogonal de C sur (AB). Par extension, on considère que [HA] et [HB] sont les projections orthogonales de [CA] et [CB] sur (AB).
Le théorème de Thales suisse affirme alors que 
, d’où que 
.
Explications :
Dans le triangle ACH rectangle en H : 
.
Dans le triangle BCH rectangle en H : 
.
Dans le triangle ABC rectangle en C : 
.
Par ailleurs : 
.
ce qui donne : 
.
Après simplification il reste : .
Remarque : cette propriété a été baptisée Théorème de Thales par les mathématiciens suisses, d’où son nom.
Autre explication :
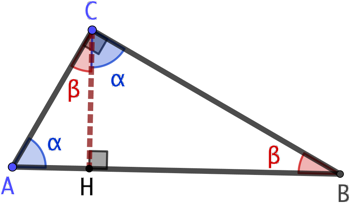
On sait que une hauteur d’un triangle rectangle le divise en deux autres triangles rectangles semblables entre eux et avec le premier. Par conséquent on a l’égalité des rapports : 
ce qui donne .
Voir aussi : racine carrée d’un nombre
