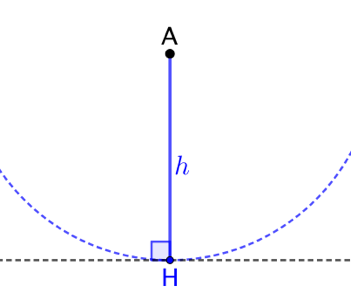
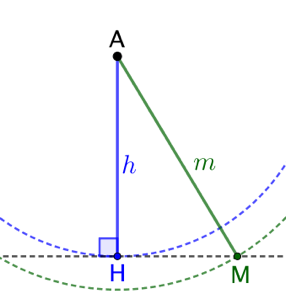
Triangle connaissant les longueurs d’un côté, de la hauteur et de la médiane correspondantes

On veut tracer un triangle ABC connaissant la longueur a du côté [BC], les longueurs de la hauteur h et de la médiane m issues de A.

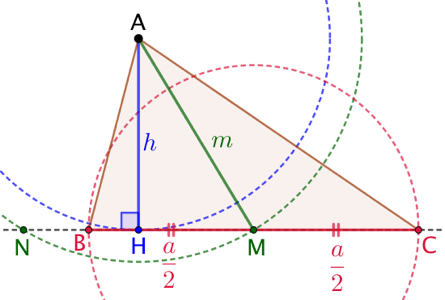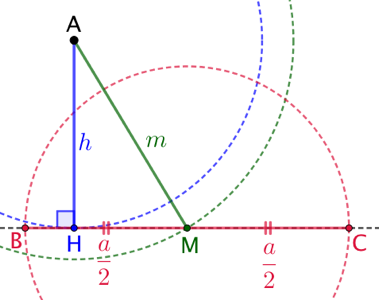
On place le point A. On trace une droite passant par A puis un cercle de centre A et de rayon a. Soit H l’intersection de cette droite et du cercle. Alors AH = h. Les deux autres sommets du triangle sont nécessairement sur la droite perpendiculaire à (AH) et passant par H.

On trace un cercle de centre A et de rayon m. Il coupe la droite passant par H en un point M qui est le milieu du côté [BC]. On trace un cercle de centre M et de rayon \dfrac{a}{2} pour obtenir les points B et C. On pouvait choisir pour le point M la position du point N.

Condition d’existence du triangle : la longueur choisie pour la médiane doit être supérieure ou égale à celle de la hauteur : m \ge h.

Print Friendly, PDF & Email