Triangle dont on connaît la base et deux hauteurs

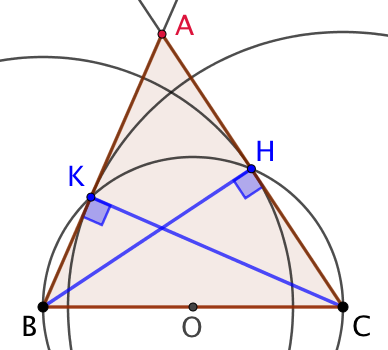
Construire un triangle ABC connaissant les longueurs du côté BC et des hauteurs issues de B et de C et de pied respectif H et K.

Construction :

1. On trace le segment [BC]
2. On place O le milieu de [BC]
3. On trace le cercle de centre O et de diamètre BC
4. On trace le cercle de centre B et de rayon BH. Le point d’intersection de ces deux cercles est le point H.
5. On trace le cercle de centre C et de rayon CK. L’intersection de ce cercle avec le cercle de centre O est le point K.
6. L’intersection des droites (BK) et (CH) est le point A.

Explications :

On utilise la propriété qui veut qu’un triangle rectangle est inscrit dans un cercle de diamètre égal à la longueur de son hypoténuse et passant par les deux extrémités de celle-ci.