Étant donnés un rectangle ABCD de dimensions 
et 
, un point E de [DC] tel que 
, le triangle ABE est isocèle en A.
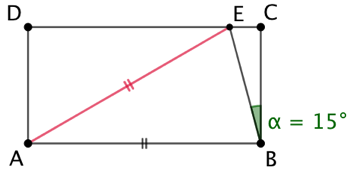
Explications : On va démontrer que 
On va déterminer la valeur de 
à l’aide du résultat suivant : 
en posant 
.
soit : 
.
Cette équation possède deux racines dont la positive est 
.
Par conséquent : 
. On a donc bien vérifier que 
. Le triangle ABE est isocèle en A. C’est un triangle d’or.
