On construit un triangle isocèle ABC de sommet C pour lequel on connait la longueur de la base et celle des deux autres côtés :
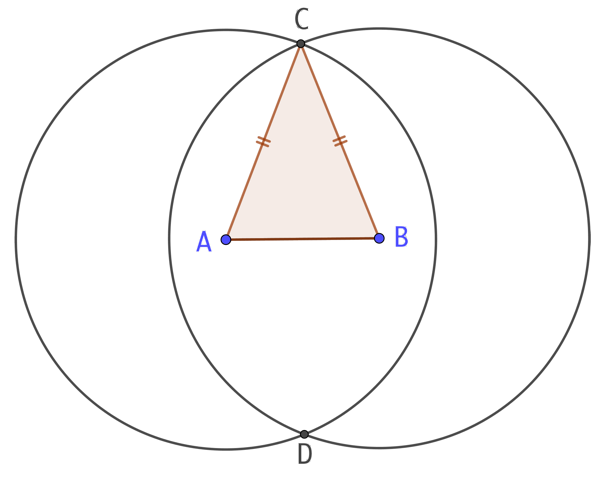
- on trace la base du triangle AB.
- On trace le cercle de centre A et de rayon AC puis le cercle de centre B et de même rayon.
- Ces deux cercles se coupent en deux points. Notons C l’un de ces points. Le triangle ABC est isocèle. On remarque que ce protocole nous permet de tracer un second triangle isocèle : ABD, de mêmes dimensions que ABC.
Explications :
Ce protocole est très proche de celui de la construction de la médiatrice d’un segment. Le point C appartient par construction à la médiatrice du segment [AB], donc CA = CB. Par conséquent, ABC est isocèle en C.
