Soit un triangle ABC quelconque. On veut construire un triangle DEF isocèle en D, inscrit dans ABC, dont la hauteur 
est donnée et dont la base est parallèle à 
.
 |
 |
 |
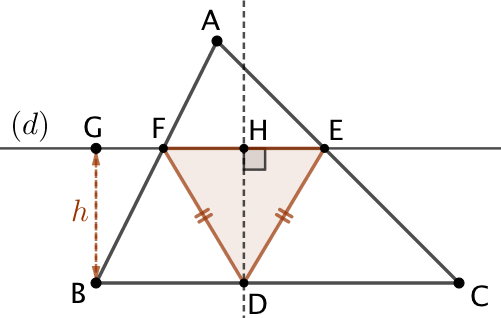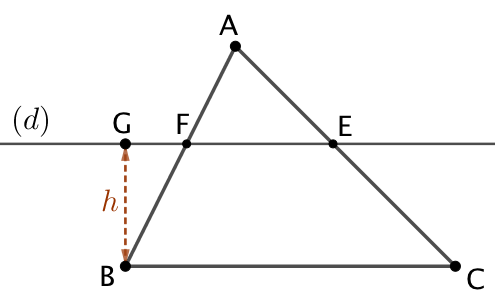
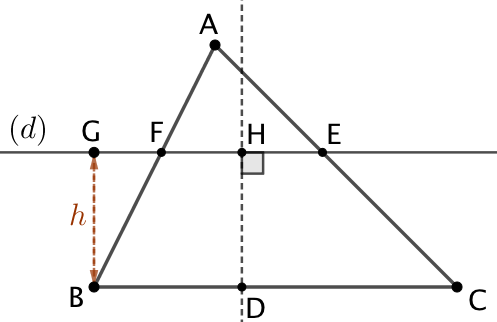
| On trace une droite (d) parallèle à (BC) et distante de h. (d) coupe le triangle en E et en F. | On trace la médiatrice du segment [EF]. Celle-ci coupe (BC) en D. | Puisque D appartient à la médiatrice de [EF], DE = DF. DEF est le triangle recherché. |
Conditions d’existence :
Il faut évidemment que la hauteur de ABC issue de A soit de longueur supérieure à h.
