I – Triangles
1) Généralités
 Un polygone est une figure plane fermée par des segments de droites.
Un polygone est une figure plane fermée par des segments de droites.
Etymologie grecque :
- polus : nombreux
- gônia : angle
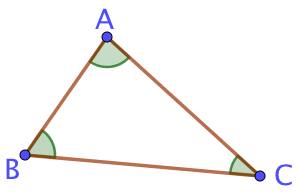
Exemple :
- Ce triangle s’appelle ABC, du nom de ses trois sommets A, B et C.
- Le point A est le sommet opposé au côté [BC].
- Le segment [BC] est le côté opposé au sommet A.
2) Construction d’un triangle
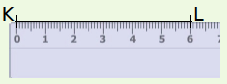
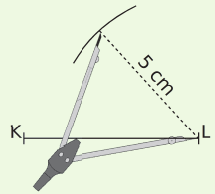
On veut construire un triangle KLM tel que KL = 6 cm, LM = 5 cm et KM = 4,5 cm.
 |
 |
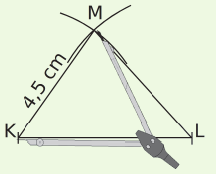 |
| On trace un segment [KL] de longueur 6 cm. | Le point M est à 5 cm du point L : il appartient donc au cercle de centre L et de rayon 5 cm. | Le point M est à 4,5 cm du point K : il appartient donc au cercle de centre K et de rayon 4,5 cm. Le point M est le point d’intersection des deux arcs. |
3) Hauteurs d’un triangle
Exemples :
| La droite |
 |
| La droite Selon la forme du triangle, une hauteur peut se situer en dehors du triangle. |
 |
II – Triangles particuliers
1) Triangle isocèle
Étymologie grecque :
- isos : égal
- skelos : jambe
- Le sommet commun aux côtés de même longueur est appelé le sommet principal.
- Le côté opposé au sommet principal est appelé la base.
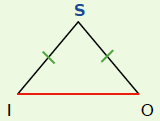 Exemple :
Exemple :
Le triangle ISO est isocèle en S donc les longueurs IS et SO sont égales. S est le sommet principal du triangle ISO. [IO] est la base du triangle ISO.
2) Triangle équilatéral
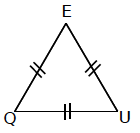 Un triangle équilatéral est un triangle dont les trois côtés sont de même longueur.
Un triangle équilatéral est un triangle dont les trois côtés sont de même longueur.
Étymologie latine :
- equus : égal
- latus : côté
Remarque : un triangle équilatéral est un triangle isocèle particulier.
3) Triangle rectangle
 Exemple :
Exemple :
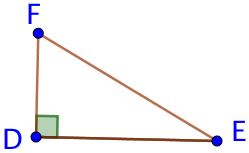
- DEF est un triangle rectangle en D. L’angle en D est droit.
- Le côté [EF] est l’hypoténuse du triangle rectangle.
III – Quadrilatères particuliers
Étymologie latine :
- quatuor : quatre
- latus : côté
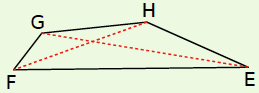 Exemple :
Exemple :
- EFGH est un quadrilatère.
- Le sommet opposé au sommet E est le sommet G.
- Un côté consécutif au côté [FG] est le côté [EF] ou le côté [GH].
- Ses diagonales sont les segments [EG] et [HF].
1) Losange
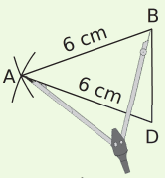
Exemple : On veut construire un losange ABCD tel que AB = 6 cm (un côté) et BD = 4,2 cm (une des deux diagonales).
 |
 |
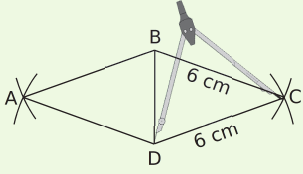 |
| On trace un segment [BD] de longueur 4,2 cm. | On construit un triangle ABD isocèle en A tell que AB = AD = 6 cm. | On construit le triangle CBD isocèle en C tell que CB = CD = 6 cm. |
2) Rectangle
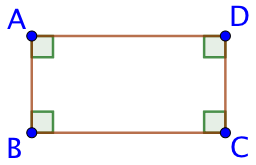 Un rectangle est un quadrilatère qui a ses quatre angles droits.
Un rectangle est un quadrilatère qui a ses quatre angles droits.
Étymologie latine :
- rectus : droit
- angulus : angle
3) Carré
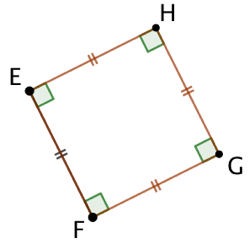 Un carré est un quadrilatère qui a ses quatre côtés de même longueur et ses quatre angles droits.
Un carré est un quadrilatère qui a ses quatre côtés de même longueur et ses quatre angles droits.
Un carré est à la fois un rectangle et un losange.
