Un carré dans un triangle

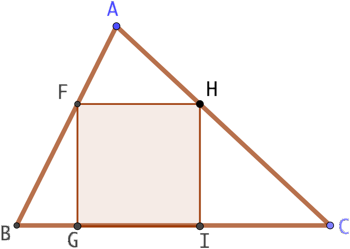
Étant donné un triangle ABC, comment placer un carré FGIH tels que

F soit sur le segment [AB],
H sur le segment [AC],
G et I sur le segment [BC] et
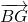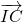les vecteurs $\overrightarrow{BG}$ et $\overrightarrow{IC}$ aient le même sens ?

Construction :

On abandonne provisoirement la contrainte « H est sur [AC] ».
On place une point F quelconque sur [AB] et on trace un carré FGIH.
Quand F parcourt le segment [AB], H se déplace sur une droite.
Le point H recherché est l’intersection de cette droite avec (AC).

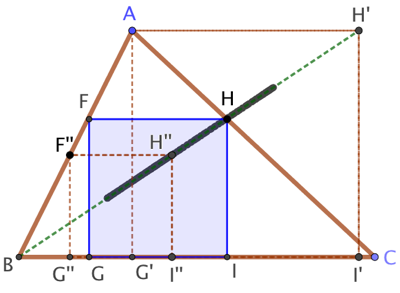Explications :

Soit G’ le pied de la hauteur issue de A. On trace le carré AG’I’H’ de côté AG’.

Soit $F''$ un point quelconque sur [AB]. La perpendiculaire de (BC) passant par $F''$ coupe (BC) en $G''$ . On trace le carré $F''G''I''H''$ de côté $F''G''$ .

Il existe une homothétie $h$ permettant de passer de $AG'I'H'$ à $F''G''I''H''$ . $h(A)=F''$ et $h(G')=G''$ .

Le centre de cette homothétie est le point B qui est le point d’intersection des droites $(F''A)$ et $(G'G'')$ .

Nécessairement $h(H')=H''$ et les point $B, H'' et H'$ sont alignés. Quand F parcourt le segment [AB], le point H suit la droite (BH’). Cette droite coupe la droite (AC) au point H recherché.

Solution cartésienne :

Pour simplifier les calculs, on choisit un repère dont le centre est B et l’unité est la longueur BC. Dans ce repère les coordonnées de A sont $(a;b)$ et celles de G sont $(g;0)$ .