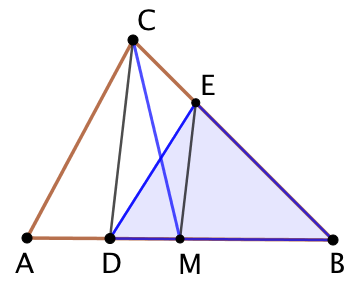
Un curieux partage d’un triangle en deux aires égales

Soient ABC un triangle et un point D mobile sur [AB]. Ou faut-il placer le point E pour l’aire du triangle DBE soit la moitié de l’aire de ABC ?

Construction :

  1. On trace la médiane issue de C qui coupe (AB) en M.
  2. On trace la droite (CD) et sa parallèle passant par M.
  3. E est le point d’intersection de cette parallèle avec (BC).

Explications :

(CM) est la médiane de ABC issue de C donc elle coupe ABC en deux triangles de même aire : AMC et MBC. Donc Aire_{MBC} = \dfrac{Aire_{ABC}}{2}.

Les triangles DME et MEC ont la même aire car ils possèdent la même base [ME] et leurs sommets respectifs C et D sont situés sur une parallèle à (ME).

Ainsi Aire_{DBE} = Aire_{DME} + Aire_{MBE} = Aire_{MEC} + Aire_{MBE} = Aire_{MBC}

Conclusion Aire_{DBE}= \dfrac{Aire_{ABC}}{2}

Remarque : Cette construction n’est valable que si D est mobile sur [AM]. Au delà de M, le point E se situe sur le [AC], mais la démonstration est identique.

Print Friendly, PDF & Email