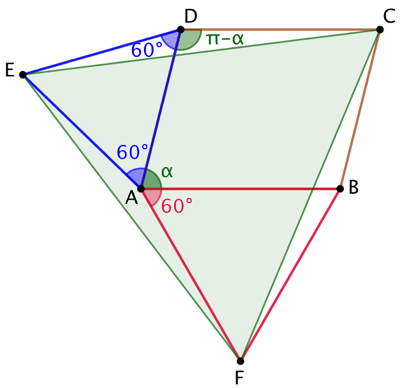
Soient ABCD un parallélogramme et les triangles équilatéraux ADE et ABF. On montre que CEF est aussi un triangle équilatéral.
Explications :
Montrons que AC = EF. Pour cela on va démontrer que les triangles ECD et EFA sont isométriques.
Soit 
la mesure de l’angle 
. Alors la mesure de l’angle rentrant 
est : 
. Donc celle de l’angle rentrant est : 
.
Or la mesure de l’angle saillant 
est : 
. Ainsi les angles et ont la même mesure.
Par construction EA = ED et AF = DC. Puisque les triangles ECD et EFA ont deux côtés, deux à deux de même longueur, entourant deux angles de même mesure, ils sont isométriques. On en conclut que leurs troisièmes côtés sont de même longueurs.
On démontre très facilement que EC = CF. Ce qui achève de démontrer que CEF est équilatéral.
