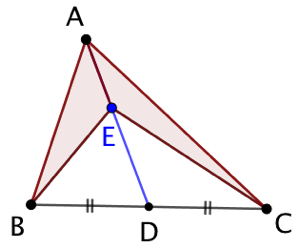
Soit un triangle ABC. Un point E, intérieur au triangle, se situe sur la médiane issue de A si et seulement si les triangles ABE et ACE possèdent la même aire.
Explications : Soit D le milieu du côté [BC].
Première partie : Supposons que E soit sur la médiane [AD].
Les triangles EBD et ECD possèdent la même aire puisque dans le triangle EBC, [ED] est la médiane du triangle issue de E.
Les triangles ABD et ACD ont la même aire. Par soustraction d’aires, il vient que les triangles ABE et ACE ont la même aire.
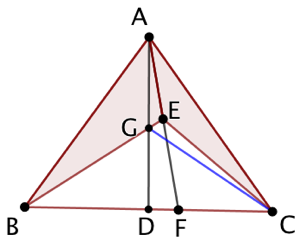Deuxième partie : Supposons que les triangles ABE et ACE possèdent la même aire et que E ne se situe pas sur la médiane de [BC] (raisonnement par l’absurde). Soit F le point d’intersection de (AE) et (BC). Nécessairement D (toujours milieu de [BC]) et F ne sont pas confondus. Enfin G est l’intersection de (BE) et de la médiane (AD).
On observe les inégalités strictes : 
et 
.
Or 
, donc les deux inégalités précédentes conduisent à 
. Cette inégalité stricte est impossible puisque G appartient à la médiane. D’après la première partie des explications, on a nécessairement 
.
Conclusion : D et F sont confondus et E appartient à la médiane (AD).
