On fait apparaître la fraction 1/3 grâce à deux triangles équilatéraux ainsi :
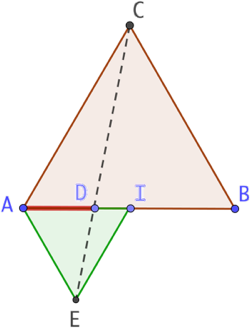
- On construit un premier triangle équilatéral ABC.
- On construit un second triangle équilatéral AEI dont le côté vaut deux fois moins que le premier.
- On trace le segment [CE]. Il coupe [AB] au point D. La distance AD mesure un tiers de AB.
Explications :
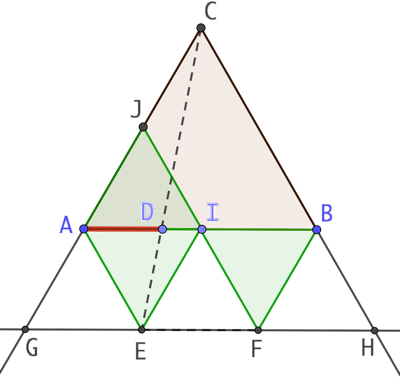
On complète la figure avec :
- un second triangle IFB de côté de même longueur que celui de AEI ;
- la droite (EF) qui coupe (AB) en G et H.
On applique le théorème de Thales sur le triangle CGE puisque les droites (AB) et (GH) sont parallèles :
AD / GE = CA / CG. Par construction, nous savons que AG = 1/3 de CG, donc CA = 2/3 de CG. Par conséquent AD / GE = 2/3 ou AD = 2/3 x GE.
Or par construction GE = AI = AB / 2. Donc AD = 2/3 x AB / 2 = AB / 3. La distance AD mesure un tiers de AB
