Un tiers plus simple

On construit un segment dont la longueur vaut le tiers de celle d’un segment [AB] ainsi :

1. On construit deux cercles de rayon AB et de centres A et B.
2. On trace la demi-droite [CA). Elle coupe l’un des cercles au point D.
3. On trace le segment [BD] et on place le point E milieu de [BD].
4. On trace le segment [CE]. Il coupe le segment [AB] au point F. La distance AF représente le tiers de la distance AB.

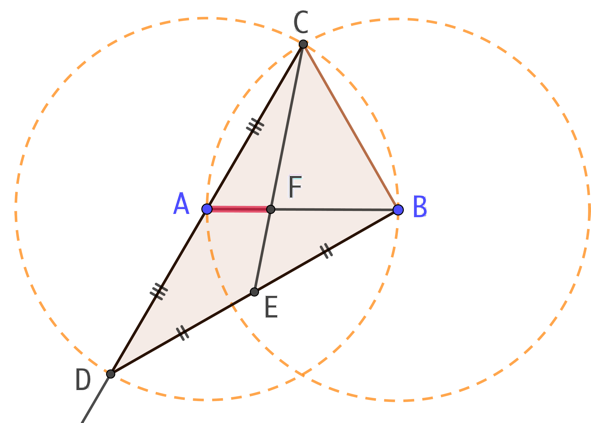
Explications :

On considère le triangle BCD.

Le segment [CD] est un diamètre du cercle de centre A, donc A est le milieu de [CD] et par conséquent [AB] est la médiane issue de B.

E est le milieu de [BD] donc [CE] est la médiane issue de C. Les deux médianes se coupent au point F. F est le centre de gravité du triangle et nous pouvons affirmer alors que la distance AF représente le tiers de la distance AB.